# 描述性统计的指标

作者：Seiya

时间：2020 年 09 月 22 日

# 描述性统计的指标

# 1、集中趋势指标

体现数据的集中趋势的指标：平均值、中位数、众数

平均值

平均值也叫均值，就是将所有数字相加再除以数字的个数。

• 平均值的计算公式

  $u = \frac{1}{N} \sum _{i=1} ^N X _{i} = \frac{1}{N}(X _{1} + X _{2} + ... + X _{N})$

• 平均值的优缺点

  • 优点：充分利用所有数据，适用性强。（生活中随处可见它的用途。）

  • 缺点：容易受到极端值影响。（工资被平均，住房面积被平均，……，“被平均”俨然已经是一个热门的网络用语。什么是极端值？比如说，马云、王健林的工资，……）

分位数

常用的分位数有中位数和上、下四分位数。

• 中位数

  • 什么是中位数？

    顾名思义，中位数就是在中间位置的数字。

  • 怎样确定中位数？

    1. 先把所有数字从小到大排个序；2. 找出中间位置的数字。

  • 中位数的优缺点

    • 优点：不受极端值影响

      和平均值相比，中位数不容易受到极端值的影响。如果平均值与中位数差距很大，那我们就需要检查一下是不是有极端值在影响了。

    • 缺点：对极端值缺乏敏感性

• 四分位数

  四分位数相当于数据被中位数分成两部分后再分别求上下两部分的中位数。

  • 上、下四分位数的用途

    • 构建箱线图，比较不同组别的数据

    • 识别异常值

• 箱线图

  • 什么是箱线图

    箱线图可以用图表表现出一个数据的大致分布情况。如下图所示：

    

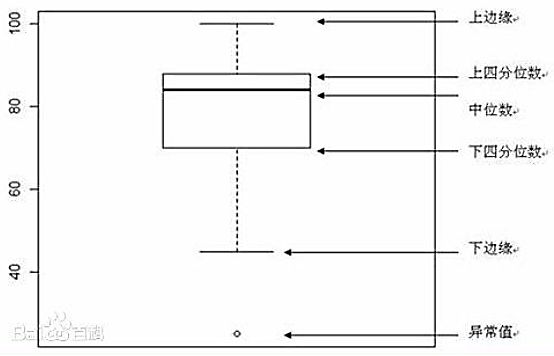
  • 箱线图的指标说明：

    • 下四分位数：Q1，将所有数据按照从小到大的顺序排序排在第 25%位置的数字

    • 上四分位数：Q3，将所有数据按照从小到大的顺序排序排在第 75%位置的数字

    • 四分位距： IQR，等于 Q3-Q1，衡量数据离散程度的一个统计量

    • 上边缘：除异常点以外的数据中的最大值（计算方式：Q3 + 1.5IQR）

    • 下边缘：除异常点以外的数据中的最小值（计算方式：Q1 - 1.5IQR）

    • 异常值：小于 Q1－k × IQR 或 大于 Q3+ k × IQR 的值

  • 箱线图的作用

    • 直观明了地识别数据批中的异常值

    • 利用箱线图判断数据批的偏态和尾重

    • 利用箱线图比较几批数据的形状

    • 箱线图可以表现出一个数据的大致分布情况。

众数

• 什么是众数？

  数据中出现次数最多的数字。

• 众数的优缺点

  • 优点

    • 均值和中位数只能用于数值型数据，而众数还能适用于非数值型数据

    • 不受极端值影响

  • 缺点

    • 众数缺乏唯一性，一组数据的众数可能有 1 个，可能有 2 个，也可能没有

# 2、离散程度指标

离散程度反映各数据远离其中心值的趋势。

数值型数据

• 极差

  一组数据的最大值和最小值之差，也称全距，用 R 表示。

  极差容易受极端值的影响，不能反映出中间数据的分散情况。

  
  

• 平均差

  平均差也称平均绝对离差、平均偏差，它是各变量值与其平均数离差绝对值的平均数。

  平均差以平均数为中心，反映了每个数据与平均数的平均差异程度。为了避免离差之和等于零而无法计算平均差这个问题，因此采取了绝对值，以离差的绝对值来表示总离差。

  
  

• 方差

  方差即是每个数值到均值距离的平方的均值。平方可以避免正负抵销。

  
  

• 标准差

  对方差开根号，使标准差的单位与计算数据的单位相同

  
  

顺序数据

• 四分位差

  上四分位数和下四分位数之差。它反映了中间 50% 的数据的离散程度，其数值越小，说明中间的数据越集中，反之则越分散。同样不受极值的影响。

分类数据

• 异众比率

  异众比率指非众数组的频数占总频数的比例。主要用于衡量众数对一组数据的代表程度。异众比率越大说明众数的代表性越差，越小说明众数的代表性越好。

相对离散程度

• 离散系数

  离散系数又称变异系数， 它是一组数据的标准差与其相应的平均数之比。

  离散系数主要用于比较不同样本数据的离散程度。离散系数大，说明数据的离散程度越大，离散系数小，说明数据的离散程度也小。