分布形态描述
作者:Seiya
时间:2020 年 09 月 23 日
数据描述的第三个维度是数据的分布形态描述,也是最为形象的描述方式,因为可以用各种统计图形将数据的分布形态形象地展现在图形上,使分析者一目了然。
事件
必然事件
在条件 S 下,一定发生的事件,叫做相对条件 S 的必然事件,简称必然事件。必然事件发生的概率为 1,但概率为 1 的事件不一定是必然事件。
不可能事件
在条件 S 下,一定不可能发生的事件,叫做相对条件 S 的不可能事件,简称不可能事件。不可能事件的概率为 0,但概率为 0 的事件不一定为不可能事件。
确定事件
必然事件和不可能事件统称为相对条件 S 的确定事件,简称确定事件。
不确定事件
在随机试验中,可能出现也可能不出现,而在大量重复试验中具有某种规律性的事件叫做不确定事件,简称随机事件。随机事件通常用大写英文字母 A、B、C 等表示。
概率
概率的产生源于事物发展的规律性及不确定性,其度量了随机事件中不同结果发生可能性的大小。
古典概率
定义
试验中所有可能出现的基本事件只有有限个;
试验中每个基本事件出现的可能性相等;具有以上两个特点的概率模型是大量存在的。
举例
抛硬币和掷骰子这两种游戏,游戏的结果种类是确定的,并且结果的发生概率都相同。
抛硬币的结果只有两种:正面和方面,每个结果的发生概率都是 1/2;掷骰子的结果有 6 种,每种结果的发生概率也都相同,都等于 1/6。
公式
统计概率法
定义
- 结果概率需要统计过往事件发生的结果频数来确定,则称为统计概率。
举例
- 在 2006 年德国世界杯的 1/4 决赛中,阿根廷与东道主德国队在 120 分钟的常规时间内打成平手,进入了残酷的点球大战。在这场令人窒息的点球大战中,德国队门神莱曼凭借守门员教练科普克递上的小纸条(上面记录着阿根廷每位点球手的踢点球习惯和射门方位,用百分数注明每位球员在过往踢点球时踢向每个方位的概率是多少),判断对了阿根廷球员射门的方向,帮助德国队淘汰阿根廷队进入决赛,并在决赛中成功击败意大利队,捧起大力神杯。
公式
主观概率法
定义
- 指根据市场趋势分析者的主观判断而确定的事件的可能性的大小,反映个人对某件事的信念程度,并不代表结果确定的发生概率。
举例
高考结束以后,高考分数在试卷交上去以后就已经确定,只是考生不知道而已。
让你魂牵梦绕的女生喜不喜欢你,这个答案女生心里早已有数,只是在你正式表白之前你不知道而已。
概率分布
概率分布指随机事件的不同结果对应其发生概率构成的分布,事件的概率分布特征可以评估样本对总体估计结果的准确性
离散型概率分布
二项分布
定义
二项分布是由伯努利提出的概念,指的是重复 n 次独立的伯努利试验。在每次试验中只有两种可能的结果,而且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试验中都保持不变,则这一系列试验总称为 n 重伯努利实验,当试验次数为 1 时,二项分布服从 0-1 分布。
特点
每次试验只有两种可能的结果:“成功”与“失败”,两个结果只会出现一个;
每次试验前,如果“成功”的概率是 p,那么"失败"的概率就是(1-p);
每次试验相互独立,每次试验结果不受其他歌词试验结果的影响;
实际应用
- 投掷骰子,大于 2 算成功,求成功的概率
多项分布
定义
等同于二项分布,唯一差别为试验结果出现 N 种
特点
每次试验有 N 种可能的结果,但是 N 种结果只会出现一个;
所有概率发生结果之和为 100%;
每次试验相互独立;
实际应用
- 试验结果确定为 2 种以上可能的事件
超几何分布
定义
超几何分布试验是在有限总体中进行无放回抽样(总体数量不断减少),所以每次试验开始前,每种试验结果发生的概率将发生变化。
特点
不同于以上两种分布,超几何分布试验结果发生的概率会随着每次试验发生改变;
从抽样层面考虑,其中二项分布是有放回的抽样,超几何分布为无放回抽样;
超几何分布可以转化为二项分布(当总体无限大时,事件发生的成功概率很小);
实际应用
- 实际应用:超市抽奖活动的中奖概率(20 个乒乓球,2 个乒乓球写有中奖)
泊松分布
定义
泊松分布考虑的是在连续时间或空间单位上发生随机事件次数的概率。基于过去某个随机事件在某段事件或某个空间内发生的平均次数,预测该随机事件在未来同样长的事件或同样大的空间内发生 n 次的概率。
特点
- 泊松分布由二项分布转化而来,当 n>=100 且 p<=0.05 时,用泊松分布近似二项分布的效果最好。
实际应用
- 根据商品(价格昂贵,需求量少)的销售历史数据,对其未来的库存进行合理控制;研究的问题是过去平均一小时有 5 人结账,接下来 1 小时有 8 人结账的概率
连续性概率分布
指数分布
定义
描述两个随机事件发生的时间间隔的概率分布,根据随机事件发生一次的平均等待时间来推断某个时间段内,随机事件发生的概率。
实际应用
- 研究过去每 20 分钟有人结账,接下来 10 分钟有人来结账的概率;
均匀分布
定义
随机事件的可能结果为连续性数据变量,所有连续性数据结果所对应的概率相等。
实际应用
- 使用均匀分布分析家具物流的送货时间(分析:组装家具的时间在固定时间范围内[25,30]min,且在该时间范围内任意时间点完成的概率相同,因此组装时间服从均匀分布)
正态分布
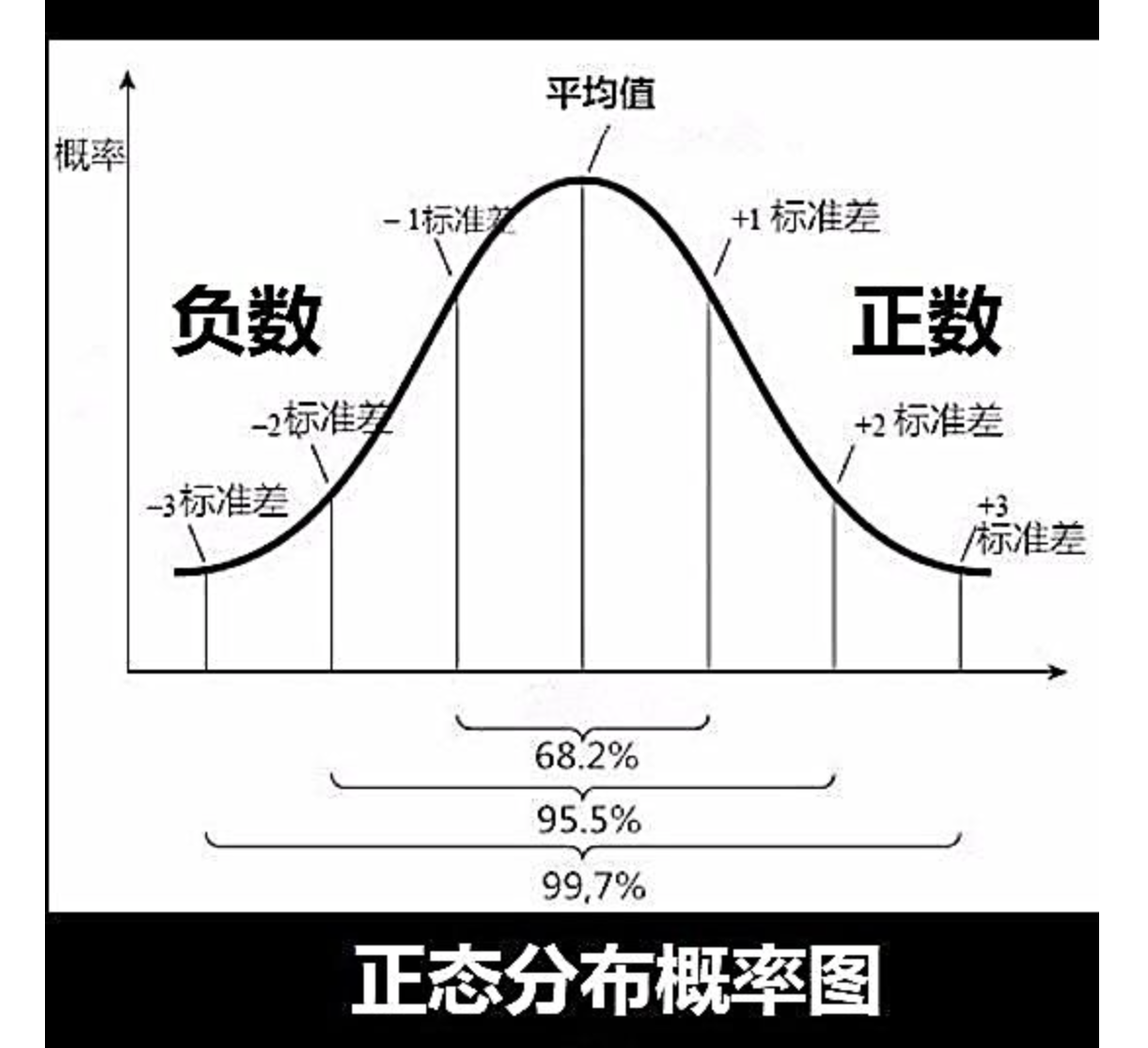
定义
表明被测事物处于稳定的状态下,测量数据的波动由偶然因素引起。即在自然环境下,自发形成稳定的系统。
实际应用
- 人的身高、体重;各种商品的尺寸和质量等
分布的形状
偏态系数
偏态是对数据分布对称性的测度。测度偏态的统计量是偏态系数,用 SK 表示。SK 的值越大,表示偏斜的程度越大。
如果一组数据的分布是对称的,离差三次方(具体公式看后面的图)后正负离差可以相互抵消,则 SK 等于 0。
如果分布是非对称的,偏态系数有正有负。SK 为正值时,表示正离差值较大,判断为正偏或右偏。
SK 为负值时,表示负离差值较大,判断为负偏或左偏。
峰态系数
峰态是对数据分布平峰或尖峰程度的测度。测度峰态的统计量是峰态系数,用 K 表示。峰态通常是相对于标准正态分布而言的:
如果一组数据服从标准正态分布,则峰态系数的值为 0;
如果峰态系数的值明显不等于 0,则表明分布比正态分布更平或更尖,称为平峰分布或尖峰分布。K 大于 0 时为尖峰分布,数据分布更集中;小于 0 时为扁平分布,数据的分布越分散。